Lớp 6 là cột mốc rất là quan trọng của những em học tập sinh. Do ở lớp này, các em phải chào đón những đưa biến new từ tâm lý đến môn trường. Vị vậy, đôi khi sẽ bị sao nhãng vấn đề học vì chưa quen phương pháp học và kiến thức và kỹ năng quá new lạ. Thấu hiểu được điều đó, trung vai trung phong gia sư WElearn đã tổng hòa hợp lại tất cả các dạng toán cải thiện lớp 6 để giúp các nhỏ bé có thể tự tín trau dồi kiến thức của bạn dạng thân.
Bạn đang xem: Các bài toán hay lớp 6
Nội dung bài xích viết1. Dạng 1: những dạng bài toán nâng cao lớp 6 về số từ nhiên2. Dạng 2: các dạng bài xích toán cải thiện lớp 6 về lũy thừa3. Dạng 3: những dạng bài toán nâng cấp lớp 6 về dấu hiệu chia hết4. Dạng 4: các dạng bài bác toán cải thiện lớp 6 về UCNN, BCLN5. Dạng 5: các dạng bài bác toán nâng cấp lớp 6 về GTNN GTLN6. Dạng 6: những dạng bài xích toán nâng cấp lớp 6 về kiếm tìm x
1. Dạng 1: những dạng bài toán cải thiện lớp 6 về số từ nhiên
1.1. Đề bài
Bài 1: tìm kiếm số thoải mái và tự nhiên có năm chữ số, hiểu được nếu viết thêm chữ số 2 vào ẩn dưới số kia thì được số mập gấp cha lần số đã có được bằng những viết thêm chữ số 2 vào đằng trước số đó.
Bài 2: search số tự nhiên và thoải mái có tận cùng bởi 3, biết rằng nếu xóa chữ số hàng đơn vị chức năng thì số đó sụt giảm 1992 đối kháng vị.
Bài 3: Tìm tía chữ số không giống nhau và khác 0, biết rằng nếu dùng cả ba chữ số này lập thành những số tự nhiên có ba chữ số thì nhị số lớn nhất có tổng bằng 1444.
Bài 4: Hiệu của nhì số là 4. Nếu như tăng một số gấp cha lần, giữ nguyên số cơ thì hiệu của | chúng bởi 60. Tìm hai số đó.
Bài 5: Tìm hai số, biết rằng tổng của bọn chúng gấp 5 lần hiệu của chúng, tích của bọn chúng gấp 24 lần hiệu của chúng.
1.2. Bài giải
Bài 1:
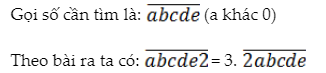
Thử lại: 857142 = 3. 285714
Vậy số nên tìm là 857142
Bài 2:
Vì rằng giả dụ xóa chữ số hàng đơn vị chức năng thì số đó sụt giảm 1992 đơn vị chức năng nên số tự nhiên và thoải mái cần tìm bao gồm 4 chữ số.
Gọi số cần tìm là abc3 (a không giống 0)
Theo đề bài xích ta có abc3 – abc = 1992
⇔ 10abc + 3 – abc = 1992 => 9abc = 1989 => abc = 221
Vậy số đề nghị tìm là 2213
Bài 3:
Gọi tía chữ số yêu cầu tìm là: a, b , c (a > b > c > 0).Theo bài ra ta có
abc + ngân hàng á châu = 1444
100a + 10b + c + 100a + 10c + b = 1444
200a + 11b + 11c = 1444
200a + 11(b + c) = 1400 + 11.4
a = 7; b =3; c =1
Vậy 3 số yêu cầu tìm là 1; 3; 7
Bài 4:
Gọi 2 số đó là a, b (a>b)
Theo bài xích ra ta có:
a – b = 4 => b = a – 4 (1)
Nếu tăng một trong những gấp bố lần, giữ nguyên số cơ thì hiệu của chúng bằng 60
3a – b = 60(2)
Thay (1) vào (2) ta có:
3a – (a – 4) = 60 => 2a = 56
a = 28 với b = 24
Vậy số cần tìm là 28; 24
Bài 5:
Theo đầu bài.
Nếu biểu lộ hiệu là một phần thì tổng là 5 phần cùng tích là 24 phần.
Số phệ là:( 5 + 1 ) : 2 = 3 ( phần )
Số bé xíu là:5 – 3 = 2 ( phần )
Vậy tích sẽ bởi 12 lần số bé.
Ta có:Tích = Số lớn x Số bé
Tích = 12 x Số bé
Suy ra Số khủng là 12
2. Dạng 2: các dạng bài xích toán nâng cao lớp 6 về lũy thừa
2.1. Đề bài
Bài 1: Tính tổng S = 1 + 2 + 22 + 23 + 24 + …+ 2100
Bài 2:

Bài 3: So sánh
536 và 112432n với 23n213 cùng 2162.2. Bài giải
Bài 1: Nhân 2 vào 2 vế, ta được

Bài 2:

Vậy đây cũng là phương pháp tính bài toán dạng S = 1 + a + a2 + … + an
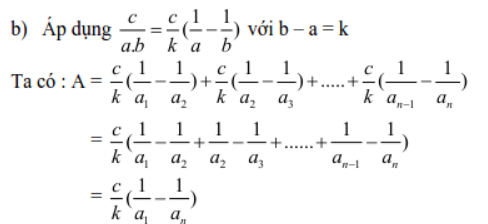
Bài 3: Ở dạng bài do sáng này, chúng ta nên đem lại cùng số mẫu mã hoặc thuộc cơ số thì mới so sánh được.
Với 2 số thuộc số mũ, số nào có cơ số lớn hơn thì số đó khủng hơn. Với 2 số cùng số cơ số, số nào có số nón lớn hơn thế thì số đó béo hơn.a. Ta có
536 = 53.12 = (53)12 = 12512
1124 = 112.12 = (112)12 = 12112
Với 2 số thuộc số mũ, số nào gồm cơ số lớn hơn nữa thì số đó bự hơn.
Vậy 536 > 1124
b. Ta có
32n = (32)n = 9n
23n = (23)n = 8n
=> 32n > 23n
c. 213 16
Vì thuộc cơ số khác số mũ
3. Dạng 3: những dạng bài xích toán nâng cao lớp 6 về tín hiệu chia hết
3.1. Đề bài
Bài 1: chứng minh: 714 – 713 + 712 phân tách hết mang đến 43
Bài 2:Cho số thoải mái và tự nhiên hai chữ số ab bằng ba lần tích của những chữ số của nó.
a/ minh chứng rằng b chia hết đến ai
b/ đưa sử b=ka (k + N), minh chứng k là mong của 10
c/ Tìm những số ab nói trên.
Bài 3: Có phép trừ hai số tự nhiên nào nhưng số trừ gấp cha lần hiệu cùng số bị trừ bằng 1030 xuất xắc không?
Bài 4: Trong những số từ bỏ nhiên nhỏ tuổi hơn 1000, gồm bao nhiêu số chia hết mang lại 2 nhưng không phân chia hết đến 5.
Bài 5: Tìm các số tự nhiên và thoải mái chia mang đến 4 thì dư 1, còn chia đưa ra 25 thì dư 3.
3.2. Bài bác giải
Bài 1
714 – 713 + 712 = 712 (72 – 7 + 1) = 712.43 phân chia hết mang đến 43
Bài 2:
a. Theo đề bài bác ta có
10a + b = 3ab
10a = b(3a – 1)
b = 10a/(3a – 1)
Vậy b phân tách hết mang lại a.
b. Ước của 10 là 5; 2 với 10
Mà b = 10a/(3a – 1) = 5.2a/(3a – 1)
Vậy b phân chia hết đến 10; 5 cùng 2
c. Vì k
TH1: k = 1. Suy ra 3a = 11 (loại) TH2: k = 2. Suy ra 6a = 12 yêu cầu a= 2 với b = 4 TH3: k = 5. Suy ra 15a = 15 yêu cầu a = 1 với b = 5Vậy tất cả hai số ab nên tìm là 24 cùng 15
Bài 3: call số trừ là x, Ta có x = 3( x – 1030) => x = 1545
Vậy có phép trừ đó
Bài 4
Số phân chia hết cho 2 tuy thế không chia hết mang lại 5 tận cùng cần là những số 2; 4; 6; 8. Như vậy, từng chục tất cả 4 số.
Từ 1 – 999 có 100 chục nên có 400 số
Bài 5:
Các số chia hết cho 25 sẽ sở hữu được tận cùng là 25; 75; 00; và 50. Vậy những số chia cho 25 dư 3 sẽ sở hữu tận thuộc là 28; 78; 03 và 53
Các số phân chia hết mang đến 4 phải bao gồm 2 số tận cùng phân chia hết cho 4.
Muốn chia chia mang đến 4 dư 1 thì 2 số tận cùng cũng bắt buộc chia 4 dư 1.
Như vậy, trong những số bên trên chỉ tất cả số 53 là thỏa điều kiện
4. Dạng 4: những dạng bài toán cải thiện lớp 6 về UCNN, BCLN
4.1. Đề bài
Bài 1: tìm số tự nhiên x, bé dại hơn 400; hiểu được x phân chia cho 4, cho 5, cho 6 đều sở hữu dư là một trong và x chia hết mang đến 7.
Bài 2:Tìm số chia và yêu thương của một phép chia có số bị chia bằng 145, số dư bằng 12 hiểu được thương khác 1 (số phân chia và mến là những số trường đoản cú nhiên).
Bài 3: Tìm nhì số tự nhiên liên tiếp có tích bởi 600.
Bài 4: Tìm hai số tự nhiên, biết rằng tổng của chúng bằng 84, ƯCLN của chúng bởi 6.
Bài 5: Tìm nhị số tự nhiên a, b > 0, biết ab = 216 và (a, b) = 6
4.2. Bài bác giải
Bài 1: vì chưng x phân tách cho 4, mang lại 5 và mang lại 6 hồ hết dư là 1 trong nên:
(x–1)⋮4;(x–1)⋮5;(x–1)⋮6
BC(4,5,6)=0,60,120,180,240,…
Bài 2: call x là số chia, a là thương, ta có
145 = ax + 12 (x>12).
Như vậy, x là mong của 145 – 12 = 133.
Phân tích ra quá số nguyên tố: 133 = 7.19
Ước của 133 mà to hơn 12 là 19 với 133.
Nếu số chia bằng 19 thì thương bằng 7.
Nếu số chia bằng 133 thì thương bởi 1 (trái cùng với đề bài).
Vậy số chia bằng 19 cùng thương bằng
Bài 3: Ta có
600 = 23.3.52 = 8.3.25 = 24.25
Vậy 2 số nên tìm là 24 cùng 25
Bài 4
Gọi nhì số nên tìm là a cùng b ( a ≤ b ).
Ta gồm (a, b) = 6 buộc phải a= 6a’, b = 6b’ trong những số đó (a’, b’) = 1 (a, a’, b, b’ N).

Do a + b = 84 đề xuất 6(a’ + b’ ) = 84 => a’ + b’ = 14. (a’ ≤ b’) ta được:
Bài 5: đưa sử a ≤ b, vì chưng (a, b) = 6 nên a = 6m, b =6n cùng với m, n nằm trong N*
(m, n) = 1 cùng m ≤ n => ab = 6m.6n = 36mn
vì ab = 216 nên 36mn = 216 => mn = 6
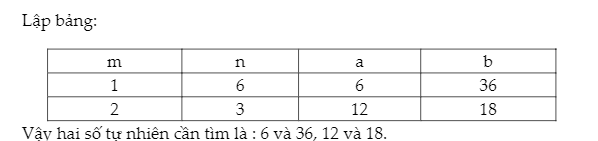
5. Dạng 5: những dạng bài xích toán cải thiện lớp 6 về GTNN GTLN
5.1. Đề bài
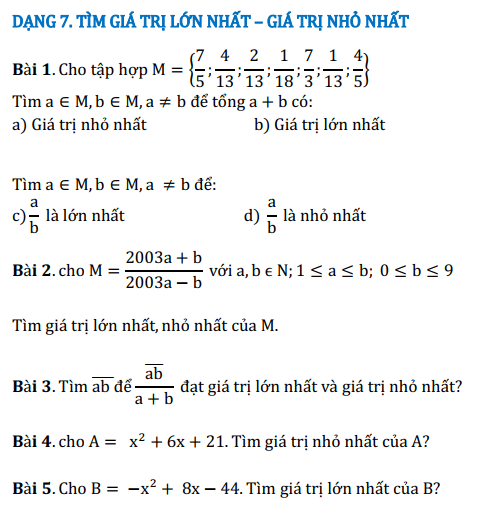
5.2. Bài xích giải
Bài 1

Bài 2

Bài 3

Bài 4
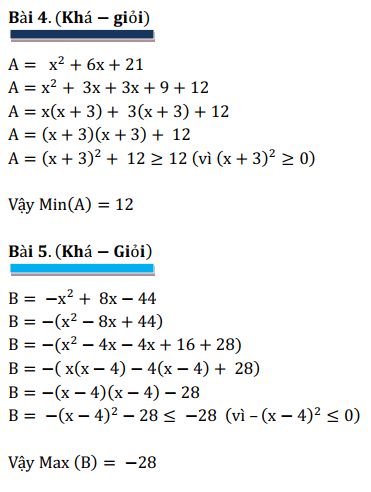
6. Dạng 6: những dạng bài toán nâng cấp lớp 6 về tìm kiếm x
6.1. Đề bài
Bài 1: tìm kiếm số thoải mái và tự nhiên x làm sao cho x – một là ước của 12
Bài 2: kiếm tìm x
4.( 2x + 7) – 3.(3x – 2) = 24|2x + 3| = 5Bài 3: tìm số x làm thế nào để cho A = 12 + 45 + x phân chia hết mang lại 3
Bài 4: kiếm tìm x để A nguyên
6.2. Bài xích giải
Bài 1:
x – 1 là ước của 12 => 12 chia hết cho (x – 1)
Ước của 12 là 2; 4; 3; 6; 12
Vậy
x – 1 = 2 => x = 3x – 1 = 4 => x = 5x – 1 = 6 => x = 7x – 1 = 12 => x = 13Bài 2:
4.( 2x + 7) – 3.(3x – 2) = 248x + 28 – 9x + 6 = 24
– x = 2 => x = – 2
Nhân chéo cánh 2 vế ta được-7(x – 34) = -21x
⇔ -7x + 21x = 238 => x = 17
Dạng trị hoàn hảo và tuyệt vời nhất này bao gồm 2 ngôi trường hợpTrường vừa lòng 1: 2x + 3 = 5 => x = 1
Trường thích hợp 2: 2x + 3 = -5 => x = -4
Bài 3: A =12 + 45 + x = 57 + x
Vì 57 chia hết đến 3 bắt buộc để A phân tách hết cho 3 thì x nên chia hết đến 3
=> x = 3k (với k là số nguyên)
Bài 4:
Để A nguyên thì 3 buộc phải chia hết mang lại x – 1
=> x – một là ước của 3
Ước của 3 là một trong và 3
=> x – 1 = 1 hoặc x – 1 = 3
=> x = 0 hoặc x = 4
Bên trên là Tổng Hợp những Dạng Toán nâng cấp Lớp 6 Đầy Đủ Nhất. chúng ta học sinh rất có thể tham khảo để nâng cấp kiến thức của mình.
? Trung trung khu gia sư WElearn chăm giới thiệu, cung cấp và thống trị Gia sư.? Đội ngũ Gia sư với trên 1000 gia sư được kiểm duyệt kỹ càng.? tiêu chuẩn của cửa hàng chúng tôi là nhanh CHÓNG cùng HIỆU QUẢ. Cấp tốc CHÓNG tất cả Gia sư với HIỆU QUẢ vào giảng dạy.
Các việc nâng cao lớp 6 thường gặp với lưu ý và bám sát đít theo khung lịch trình sách giáo khoa Toán lớp 6, những bài giải bài xích tập Toán 6 tương xứng với từng bài học trong sách giúp cho các em học sinh ôn tập cùng củng cố các dạng bài xích tập, rèn luyện kĩ năng giải Toán 6.
1. Đề bài bác Bài tập Toán nâng cao lớp 6
Câu 1: Số vừa là bội của 3 vừa là mong của 54 là?
Câu 2: Cho phường là tập hợp những ước ko nguyên tố của số 180. Số phần tử của tập hợp p là?
Câu 3: tía số nguyên tố tất cả tổng là 106. Trong những số hạng đó, số nguyên tố lớn số 1 thỏa mãn rất có thể là…
Câu 4: bao gồm bao nhiêu số chẵn có 4 chữ số
Câu 5: mang lại đoạn trực tiếp OI = 6. Trên OI mang điểm H sao cho HI = 2/3OI. Độ nhiều năm đoạn trực tiếp OH là…….cm.
Câu 6: Số từ bỏ nhiên nhỏ dại nhất (khác 0) phân chia hết cho tất cả 2; 3; 5 và 9 là ………….
Câu 7: dịp 8 giờ, một bạn đi xe đạp từ A cho B bí quyết A một khoảng 10km. Biết rằng bạn đó mang đến B lúc 10 giờ đồng hồ 30 phút. Tốc độ của tín đồ đi xe đạp là……….km/h.
Câu 8: một tấm học tất cả 40 học tập sinh tạo thành các nhóm, mỗi nhóm nhiều nhất 6 học tập sinh. Hỏi số nhóm ít nhất hoàn toàn có thể là ...
Câu 9: Một người đi dạo mỗi phút được 60m, người khác đi xe đạp mỗi tiếng được 24km. Tỉ số xác suất vận tốc của người đi dạo và tín đồ đi xe đạp là ……….%.
Xem thêm: Review yoga thiền trái tim vàng chưa, e xin ý kiến ạ!, yoga và thiền golden hearts group
Câu 10: tổng cộng tuổi của hai bạn bè là 30 tuổi. Biết tuổi em bởi 2/3 tuổi anh. Tuổi anh hiện giờ là ……...
Câu 11: Viết thường xuyên các số thoải mái và tự nhiên từ 1 mang đến 100 ta được số có……..chữ số.
Câu 12: Một fan đi quãng mặt đường AB vận tốc 15/km bên trên nửa quãng đường đầu và gia tốc 10/km trên nửa quãng mặt đường sau. Vận tốc trung bình của tín đồ đó bên trên cả quãng mặt đường AB là …..km/h.
Câu 13: Một tháng có ba ngày công ty nhật rất nhiều là ngày chẵn. Ngày 15 tháng chính là thứ………
Câu 14: bây giờ tuổi anh gấp gấp đôi tuổi em, từ thời điểm cách đây 6 năm tuổi anh vội 5 lần tuổi em. Tổng cộng tuổi của 2 đồng đội hiện ni là
Câu 15: Tính diện tích một hình tròn, biết nếu giảm đường kính hình tròn trụ đó đi 20% thì diện tích s giảm đi 113,04 cm2
Câu 16: Hãy cho biết có từng nào số thập phân gồm 2 chữ số tại đoạn thập phân mà lớn hơn 24 và nhỏ tuổi hơn 25?
Câu 17: phân chia 126 cho một số trong những tự nhiên a ta được số dư là 25. Vậy số a là
Câu 18: gồm bao nhiêu số tự nhiên có 4 chữ số?
Có bao nhiêu số chẵn gồm 3 chữ số?
Câu 19: tìm số từ bỏ nhiên nhỏ nhất biết rằng khi phân chia số này đến 29 thì dư 5 và chia cho 31 dư 28
Câu 20: hotline A là tập hợp cầu của 154. A gồm số tập hợp con là?
Câu 21:
a. Có toàn bộ bao nhiêu phương pháp viết số 34 dưới dạng tổng của nhị số nguyên tố? Trả lời:……cách.
b. Có……số vừa là bội của 3 với là ước của 54
Số các ước thoải mái và tự nhiên có hai chữ số của 45 là
Câu 22:
Câu A. lúc chia một trong những tự nhiên đến 4 được số dư là 2. Số dư trong phép phân chia số tự nhiên và thoải mái đó cho 2 là
Câu B: Một lớp học gồm 40 học tập sinh chia thành các nhóm, mỗi nhóm nhiều nhất 6 học sinh. Hỏi số đội ít nhất có thể là
Câu C: mang đến hình chữ nhật ABCD có chiều lâu năm là 12cm, chiều rộng lớn là 8cm. Diện tích s hình tam giác ABC là
Câu D: Trong một phép chia, nếu ta gấp rất nhiều lần số phân chia thì mến của phép chia cũ vội vàng lần đối với thương của phép phân chia mới.
Câu E: mang đến tam giác ABC.Trên cạnh AB rước điểm M, bên trên cạnh AC mang điểm N làm sao cho AM bởi 1/3 AB. NC bởi 2/3 AC. Diện tích hình tam giác ABC gấp diện tích s hình tam giác AMN số lần là....................
Câu F: Tổng của nhì số thoải mái và tự nhiên là 102. Trường hợp thêm chữ số 0 vào bên nên số bé rồi cùng với số to ta được tổng new là 417. Vậy số bự là .
Câu G: Một người đi dạo mỗi phút được 60m, fan khác đi xe đạp mỗi giờ đồng hồ được 24km. Tỉ số xác suất vận tốc của người quốc bộ và fan đi xe đạp là %.
Câu H: Một fan đi quãng mặt đường AB gia tốc 15km/giờ bên trên nửa quãng con đường đầu và vận tốc 10km/giờ bên trên nửa quãng mặt đường sau. Tốc độ trung bình của bạn đó bên trên cả quãng con đường AB là.
Câu I: Tỉ số của 2 số là 7/12, thêm 10 vào số trước tiên thì tỉ số của chúng là 3/4. Tổng của 2 số là?
Câu K: Một tháng có bố ngày nhà nhật phần lớn là ngày chẵn. Ngày 15 tháng sẽ là thứ
Câu 23: Viết số 43 dưới dạng tổng nhị số nguyên tố a, b cùng với a
Câu 26: Có toàn bộ bao nhiêu giải pháp viết số 34 bên dưới dạng tổng của nhì số nguyên tố? Trả lời: Cách...
Câu 28: Có bao nhiêu hợp số bao gồm dạng

Câu 29: Tìm số nguyên tố P sao để cho P+ 2 với P+ 4 cũng là số nguyên tố. Kết quả là P=
Câu 30: Số 162 tất cả tất cả………ước.
Câu 31: Cho p là tập hợp các ước ko nguyên tố của số 180. Số thành phần của tập hợp p là……
Hãy điền số phù hợp vào chỗ .... Nhé !
Câu 32: Tổng 5 số nguyên tố đầu tiên là ………..
Tham khảo các dạng Toán lớp 6
2. Giải bài bác tập Toán cải thiện lớp 6
Câu 1: các số là bội của 3 là: 0; 3; 6; 9; 12; 15; 18; 21; 24; 27; 30; 33; 36; 39; 42; 45; 48; 51; 54; 57;....
Các số là cầu của 54 là: 1; 2; 3; 6; 9; 18; 27; 54.
Các số vừa là bội của 3 vừa là ước của 54 là: 3; 6; 9; 18; 27; 54
Vậy gồm 6 số vừa là bội của 3 vừa là cầu của 54
Câu 2: 180 = 22 x 32 x5
Số ước 180 là: 3 x 3 x 2= 18 ước.
Các ước nguyên tố của 180 là: 2;3;5 có 3 ước.
Số ước không thành phần của 180 là: 18 - 3 = 15 ước.
Câu 3: cha số nguyên tố có tổng là 106 phải trong ba số này phải có 1 số chẵn => Trong bố số nguyên tố cần tìm có 1 số hạng là số 2.
Tổng nhị số còn lại là 106 - 2 = 104.
Gọi 2 số nguyên tố còn lại là a và b (a > b).
Ta có a + b = 104 => Để số a là số nguyên tố lớn nhất nhỏ nhất thì b phải là số nguyên tố nhỏ nhất.
Số nguyên tố b nhỏ nhất là 3 => a = 104 - 3 = 101 cũng là 1 số nguyên tố (thỏa mãn yêu cầu đề bài).
Vậy số nguyên tố lớn nhất thỏa mãn yêu thương cầu đề bài là 101.
Câu 4: Số lớn nhất 9998
Số nhỏ bé nhất 1000
Có: (9998 - 1000) : 2 + 1 = 4500 (số)
Câu 5 | Câu 6 | Câu 7 | Câu 8 | Câu 9 | Câu 10 | Câu 11 | Câu 12 | Câu 13 |
2 | 90 | 4 | 7 | 15% | 18 | 192 | 12 | 7 |
Câu 14: Anh 16, em 8
Câu 15: giảm đường kính đi 20% thì bán kính cũng giảm xuống 20%
bán kính của hình tròn trụ mới là 100% - 20%= 80%
diện tích hình tròn trụ có nửa đường kính 80% là 80% * 80% = 64%
diên tích hình tròn cũ hơn hình tròn mới là 100% * 100% - 64%= 36%
36%=113,04cm2 => diện tích hình tròn thuở đầu là 113,04: 36 * 100 = 314cm2
Câu 16: Số bé dại nhất đống ý đề bài là: 24,01
Số lớn số 1 thoả mãn đề bài là: 24,99
Từ 1 mang đến 99 có:
(99 - 1) : 1 + 1 = 99 (số)
Vậy bao gồm 99 số ưng ý đầu bài.
Câu 17:
126: a dư 25=>a không giống 0 ; 1;126
=>126-25=101 chia hết mang đến a
Mà 101=1.101
=>a=1(L) hoặc a=101(TM)
Vậy a=101
Câu 18:
Có số các số tự nhiên và thoải mái có 4 chữ số là:
(9999-1000) : 1 + 1 = 9000 (số)
Đáp số: 9000 số
Có số những số chẵn có 3 chữ số là:
(998-100) : 2 + 1 = 450 (số)
Đáp số: 450 số
Câu 19: Gọi số tự nhiên đề nghị tìm là A
Chia cho 29 dư 5 nghĩa là: A = 29p + 5 ( phường ∈ N )
Tương tự: A = 31q + 28 ( q ∈ N )
Nên: 29p + 5 = 31q + 28 => 29(p - q) = 2q + 23
Ta thấy: 2q + 23 là số lẻ => 29(p – q) cũng chính là số lẻ =>p – q >=1
Theo mang thiết A bé dại nhất => q bé dại nhất (A = 31q + 28)
=>2q = 29(p – q) – 23 nhỏ nhất
=> p. – q bé dại nhất
Do đó p. – q = 1 => 2q = 29 – 23 = 6
=> q = 3
Vậy số đề xuất tìm là: A = 31q + 28 = 31. 3 + 28 = 121
Câu 20: Để search tập hợp con của A ta chỉ cần tìm số ước của 154
Ta có:154 = 2 x 7 x 11
Số cầu của 154 là : ( 1 + 1 ) x ( 1 + 1 ) x ( 1 + 1 ) = 8 ( cầu )
Số tập hợp con của tập phù hợp A là:
2n trong những số đó n là số thành phần của tập vừa lòng A
=> 2n = 28 = 256 ( tập hợp nhỏ )
Trả lời: A gồm 256 tập vừa lòng con
Câu 21:
a | b | c |
4 | 6 | 15 và 45 |
Câu 22:
A. phân tách 4 dư 2m
Lấy 2:2 = 1 dư 0
B. 40 : 6 = 6 dư 4
Vậy ít nhất có 6 nhóm
C. Diện tích s tam giác ABC bằng nửa diện tích s hình chữ nhật ABCD

Đường chéo AC phân chia hình chữ nhật ra làm cho hai.
Hoặc tính diện tích s tam giác ABC là tam giác vuông nên diện tích s của nó = một nửa tích của hai cạnh góc vuông.
D. 2 lần
E. Nối BN.
Xét tam giác AMN với tam giác ABN bao gồm chung con đường cao hạ trường đoản cú đỉnh N xuống cạnh AB và có AM = 1/3AB
=>S AMN = 1/3 S ABN (1)
Xét tam giác ABN với tam giác ABC gồm chung đường cao hạ từ đỉnh B xuống cạnh AC và bao gồm AN = 1/3 AC
=>S ABN = 1/3 S ABC (2)
Từ (1) với (2) ta gồm : S AMN = 1/3.1/3 S ABC = 1/9 S ABC
=> S ABC = 9 S AMN
Đáp số: 9 lần
F. 67
H. Bởi nửa đoạn đường đầu bằng nửa phần đường sau => thời hạn đi tỉ trọng nghịch cùng với vận tốc.
=> Tỉ lệ vận tốc nửa đoạn đường đầu cùng nửa đoạn đường sau là 10 : 15 =

=> Gọi thời hạn đi nửa đoạn đường đầu là 2t thì thời hạn đi nửa đoạn đường sau là 3t








